200字
[大学物理] 总复习(1)
2025-12-11
2025-12-23
学校课程

本文章整理了沈黄晋所著的《大学物理学（下）》中电磁学的部分。

本文章主要包含以下章节内容：

  • 真空中的恒定磁场

  • 磁介质

  • 电磁感应

  • 电磁波

真空中的恒定磁场

恒定电流

电流定义式

I = \frac{dq}{dt}

电流密度

\vec{j} = \frac{dI}{dS}\vec{e_n}
dI = \vec{j}\cdot d\vec{S}

电流连续性方程

\oiint_S \vec{j}\cdot d\vec{S} = \oiint_S dI = -\frac{d\vec Q}{dt}

注意这个负号！

负号代表由内向外

S为导体内任意封闭平面

特别地，当 \frac{dQ}{dt} =0 ，为恒定电流。

欧姆定律

I = \frac{U}{R} = \frac{V_1-V_2}{R}

其中

R = \rho\cdot\frac{l}{S}

\rho 为电阻率。

电导率 \sigma = \frac{1}{\rho}，单位为 \Omega^{-1}\cdot m^{-1} 。

欧姆定律微分形式：

\vec{j} = \sigma\vec{E}

电动势

\epsilon = \int^+_- \vec{F_{Ek}} \cdot d\vec{l}

负到正：内部

由于电源外没有非静电力做功，因此沿回路一圈非静电力做功也等于电动势，公式留作习题。

磁场 磁感应强度

洛伦兹力

\vec{F} = q\vec{v}\times\vec{B}

叉乘方向：符合右手螺旋定律

[重点] 毕奥─萨伐尔定律（B-S定律）

原始形式

直接写矢量形式：

d\vec{B} = \frac{\mu_0}{4\pi} \frac{Id\vec l\times\vec{e_r}}{r^2}

描述了电生磁

曲线积分形式省略，感兴趣的话可以自己写一下，此外这个不算是真正的积分，应该算叠加。

实际操作中一般是换元后可以直接求出 Id\vec l\times\vec{e_r} 的微分值，然后用另一个参数去算积分。

二级结论

载流直导线的磁场

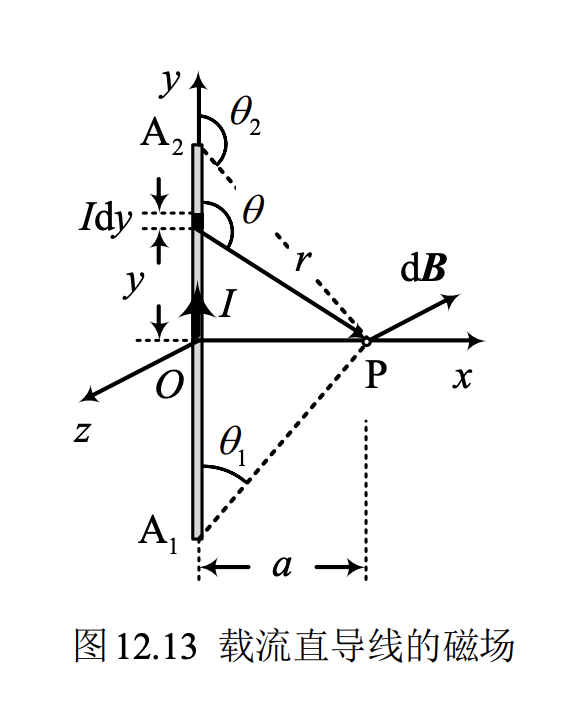
B = \frac{\mu_0I}{4\pi a}(\cos\theta_1-\cos\theta_2)

其中 \theta_1 \theta_2 按顺序为电流正方向与P点的夹角。

记忆方法（比较野）：系数和原始形式一样，分母的 r^2 变成了 a 。

令 \theta_1 = 0 \theta_2 = \pi 易证无限长载流直导线磁场：

B = \frac{\mu_0I}{2\pi a}

圆电流轴线上任意一点的磁场

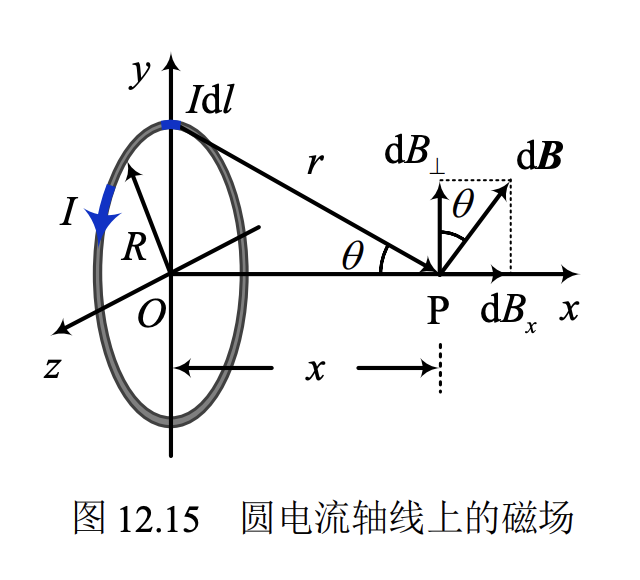
中心点有：

B_0=\frac{\mu_0I}{2R}

记忆方法： l 代入 2\pi R

轴线上其他位置有：

B = B_0\sin^3\theta

磁矩

\vec{m} = NIS\vec{e_n}

方向与电流方向符合右手螺旋定则

磁矩改写后的公式比较难记，应该也用不上，这里省略。

直螺线管轴线上的磁场

要求 l>>R 。

内部：

B=\mu_0nI

记忆方法：直接用安培环路定理推

两端：

B=\frac12\mu_0nI

其中 n 为单位长度内的匝数。

真空中恒定磁场的基本定理

磁感应线——省略

磁通量

单位：韦伯（Wb）

\Phi = \vec{B}\cdot\vec{S}

同样微分形式有：

d\Phi = \vec{B}\cdot d\vec{S}

计算曲面的磁通量求个二重积分就行，在此不过多赘述。

真空磁场的高斯定理

封闭曲面磁通量为0

[重点]真空磁场的安培环路定理

\oint_L\vec{B}\cdot d\vec{l} = \mu_0\sum I_i

或者对于电流连续分布的载流体：

\oint_L\vec{B}\cdot d\vec{l} = \mu_0\iint_S\vec{j}\cdot d\vec{S}

其中S是以闭合回路L为边界的任意曲面

可用于证明无限长的载流直导线磁场、直螺线管中的磁场

磁场对电流的作用

安培定律

d\vec{F} = Id\vec{l}\times\vec{B}

这个应该比较好记

均匀磁场对线圈的作用

\vec M = \vec{m} \times \vec{B}

这里的M是力矩， \vec m=NIS\vec e_n

具体的推导过程比较复杂，大致知道面积的引入与垂直距离有关就行。

因此经过复杂的变换之后，回归到这个叉乘上来了。

磁场力与磁力矩的功

A =NI\Delta\Phi

这个按照 N \cdot BIL \cdot \Delta x 记就行（注意只有一个N），然后做一些单位替换，推广到旋转的情况也一样，没必要手推。

（这里不确定对磁通量的理解是否正确，如果有人看到的话可以补充说明一下）

（注：解决了，和后面磁链的概念弄混了）

带电粒子的运动

洛伦兹力

前面写了。

基本运动

高中内容。

速度选择器

高中内容。

霍尔效应

注意霍尔系数的定义：

U = R_H\frac{IB}{d}

别的都显然易见，可以现推。

额外强调下

I = nevbd

就行

磁介质

磁介质的磁化

被磁化的磁介质会激发附加磁场 B' ，从而影响原磁场 B_0 的分布。

相对磁导率：

\mu_r = \frac{B}{B_0}

表示磁介质对磁场的影响程度。

弱磁介质：顺磁质 \mu_r > 1 ，抗磁质 \mu_r < 1

强磁介质：铁磁质 \mu_r >> 1

磁化具体原理与分子磁矩有关，在此不过多赘述，只需要记住顺磁质分子固有磁矩不为0，抗磁质分子固有磁矩为0。

“应当指出：顺磁质中，核外电子的轨道运动也会产生附加磁矩，产生抗磁效应。但是顺磁质中的抗磁效应远小于顺磁效应，因此在顺磁质的磁化过程中可以不考虑其抗磁效应。”

磁化强度与磁化电流

\vec M = \frac{\sum\vec p_m + \sum\vec {\Delta p_m}}{\Delta V}

式中 \sum\vec p_m 是体积 ΔV 内分子固有磁矩的矢量和， \sum\vec {\Delta p_m} 是体积 ΔV 内分子附加磁矩的矢量和。在顺磁质中， \sum\vec {\Delta p_m}忽略不计；在抗磁质中， \sum\vec {p_m} 为0。

磁化强度与磁化电流的关系

\vec{j_s} = \vec M \times \vec e_n

普遍关系：

\oint_L \vec{M} \cdot d\vec L = \sum I_s

磁介质下的安培环路定理

\vec H = \frac{\vec B}{\mu_0} - \vec M

上述式人话翻译：磁场强度就是刨去了磁化强度

类比电位移矢量：

\frac{\vec D}{\varepsilon_0} = \vec E + \frac{\vec P}{\varepsilon_0} = \vec E_0 + \vec E' + \frac{\vec P}{\varepsilon_0} = \vec E_0

环路定理也有：

\oint_L \vec{H} \cdot d\vec L = \sum I_0

磁化特性

没什么好说的

磁化强度与磁场强度成正比

\vec M = \chi_m\vec H

于是经过一系列推导（显然易见），可以得到：

\frac{\vec B}{\mu_0} = \vec H + \vec M = (1+\chi_m)\vec H = \mu_r\vec H

即

\vec B = \mu_0\mu_r\vec H = \mu\vec H

于是得到

\mu_r = 1+\chi_m \\ \mu = \mu_0\mu_r

铁磁质

了解概念就行，说简单点就是B和H的变化不再同步、也不线性——磁滞

铁磁质分类依据——磁滞回线

电磁感应

感生电动势

主要就一个公式（法拉第电磁感应公式）：

\Epsilon_i = -\frac{d\Psi}{dt}

其中

\Psi = N\Phi

称为磁链

法拉第电磁感应公式中的负号是楞次定律的体现。

动生电动势

\Epsilon = \int_L (\vec v \times \vec B) \cdot d\vec l

方向：右手定则判断或者根据公式正负号判断

感生电场

主要了解感生电场是无源非保守场就行，公式类的和前面差不多。

求电场就相当于把前面的 \Epsilon_i 换成电场和距离的积分。

自感和互感

一共就这几个公式，背就完了：

自感

\Psi = LI

解释：自感越强，磁场越强，而磁场又和电流成正比

\Epsilon_L = -L\frac{dI}{dt}

单位：亨利（H）

互感

\Psi_{21} = M_{21}I_1 \\ \Psi_{12} = M_{12}I_2

（分别是1对2的互感以及2对1的互感，即1通电在2上产生的）

而且有

M_{21} = M_{12} = M

于是有

\Epsilon_{21} = -M\frac{dI_1}{dt} \\ \mathbf{} \\ \Epsilon_{12} = -M\frac{dI_2}{dt}

单位也为亨利（H）

磁场能量

LC振荡电路：

\nu = \frac 1 {2\pi\sqrt{LC}}

自感线圈：

W_m = \frac12LI^2

磁场能量密度：

w_m = \frac12HB

电磁场与电磁波

全电流安培环路定理

\oint_L \vec H \cdot d\vec L = \iint_S \vec j_c \cdot d\vec S + \iint_S \frac{\partial\vec D}{\partial t}\cdot d\vec S

本质：变化电场也能激发涡旋磁场

麦克斯韦方程组

\left\{\begin{align} \oiint_S\vec D \cdot d\vec S &= \iiint_V \rho dV &(静电场高斯定理\rightarrow电位移矢量)\\ \oint_L \vec E \cdot d \vec L &= - \iint_S \frac{\partial B}{\partial t}\cdot d\vec S &(法拉第电磁感应)\\ \oiint_S \vec B \cdot d \vec S &= 0 &(磁场中的高斯定理) \\ \oint_L \vec H \cdot d\vec L &= \iint_S \vec j_c \cdot d\vec S + \iint_S \frac{\partial D}{\partial t}\cdot d\vec S &(全电流安培环路定理) \end{align}\right.

(1)式可以参考以下deepseek对话：https://chat.deepseek.com/share/6uzmm6ydrdzdqx4yl7

电磁波

u = \frac1{\sqrt{\mu_0\mu_r\varepsilon_0\varepsilon_r}} = \frac1{\sqrt{\varepsilon\mu}}
\sqrt{\varepsilon}E = \sqrt\mu H

真空中， u=c , \varepsilon = \varepsilon_0 。

电磁波的能量密度

电场能量密度与磁场能量密度

w_E = \frac12 \varepsilon E^2 \\ \mathbf{} \\ w_m = \frac12\mu H^2

结合电磁场关系式可得：

w = \varepsilon E^2 = \sqrt{\varepsilon\mu}EH = \frac{EH}u

易得平均能量密度：

\bar w = \frac12 \frac{E_0H_0}u

电磁波的强度

能量密度（3空间自由度） -> 能流密度（2空间自由度、1时间自由度）

由 S=wu 可推得

\vec S = \vec E \times \vec H

上述公式可以被理解为中心公式，用于推得其他需要的公式。

同样易得平均能流密度（波强）：

\bar S = \frac12 E_0H_0 = \frac12u\varepsilon E_0^2

电磁波的动量

p = \frac wc = \frac{EH}{c^2}

矢量表达式：

\vec p = \frac{\vec S} {c^2}

电磁学部分完结，接下来更新光学部分。

[数据结构] 当数据结构"遇见"C++
[大学物理] 光的衍射

Comment

© Kuri's Blog. All Rights Reserved. / RSS / Sitemap
Powered by Halo & Theme-Fuwari
鄂ICP备2025094855号-1 | 鄂公网安备42018502007857号